73. Polynomial interpolation: Newton interpolation

Anne Kværnø (modified by André Massing)

Date: Jan 18, 2021

If you want to have a nicer theme for your jupyter notebook, download the cascade stylesheet file tma4125.css and execute the next cell:

import matplotlib.pyplot as plt
import numpy as np
from IPython.core.display import HTML
from numpy import pi
from numpy.linalg import norm, solve  # Solve linear systems and compute norms


def css_styling():
    try:
        with open("tma4125.css") as f:
            styles = f.read()
            return HTML(styles)
    except FileNotFoundError:
        pass  # Do nothing


# Comment out next line and execute this cell to restore the default notebook style
css_styling()

And of course we want to import the required modules.

%matplotlib inline


newparams = {
    "figure.figsize": (6.0, 6.0),
    "axes.grid": True,
    "lines.markersize": 8,
    "lines.linewidth": 2,
    "font.size": 14,
}
plt.rcParams.update(newparams)

73.1. Newton interpolation

This is an alternative approach to find the interpolation polynomial. Let \(x_0,x_1,\ldots,x_n\) be \(n+1\) distinct real numbers. Instead of using the Lagrange polynomials to write the interpolation polynomial in Lagrange form, we will now employ the Newton polynomials \(\omega_i\), \(i=0,\ldots, n\). The Newton polynomials are defined by as follows:

\[\begin{split} \begin{align*} \omega_0(x) &= 1, \\ \omega_1(x) &= (x-x_0), \\ \omega_2(x) &= (x-x_0)(x-x_1), \\ \ldots \\ \omega_n(x) &= (x-x_0)(x-x_1)\cdots(x-x_{n-1}), \end{align*} \end{split}\]

or in more compact notation

\[ \begin{equation} \omega_i(x)= \prod_{k=0}^{i-1}(x-x_k). \label{eq:newton_poly} \tag{1} \end{equation} \]

The so-called Newton form of a polynomial of degree \(n\) is an expansion of the form

\[ p(x)=\sum_{i=0}^{n} c_i \omega_i(x) \]

or more explicitly

\[ p(x)=c_n (x-x_0)(x-x_1)\cdots(x-x_{n-1}) + c_{n-1}(x-x_0)(x-x_1)\cdots(x-x_{n-2}) + \cdots + c_1(x-x_0) + c_0. \]

In the light of this form of writing a polynomial, the polynomial interpolation problem leads to the following observations. Let us start with a single node \(x_0\), then \(f(x_0)=p(x_0)=c_0\).

Going one step further and consider two nodes \(x_0,x_1\). Then we see that \(f(x_0)=p(x_0)=c_0\) and \(f(x_1)=p(x_1)=c_0 + c_1(x_1-x_0)\). The latter implies that the coefficient

\[ c_1=\frac{f(x_1)-f(x_0)}{x_1-x_0}. \]

Given three nodes \(x_0,x_1,x_2\) yields the coefficients \(c_0,c_1\) as defined above, and from

\[ f(x_2)=p(x_2)=c_0 + c_1(x_2-x_0) + c_2(x_2-x_0)(x_2-x_1) \]

we deduce the coefficient

\[ c_2=\frac{f(x_2) - f(x_0) - \frac{f(x_1)-f(x_0)}{x_1-x_0} (x_2-x_0)}{(x_2-x_0)(x_2-x_1)}. \]

Playing with this quotient gives the much more structured expression

\[ c_2=\frac{\frac{f(x_2)-f(x_1)}{x_2-x_1} - \frac{f(x_1)-f(x_0)}{x_1-x_0}}{(x_2-x_0)}. \]

This procedure can be continued and yields a so-called triangular systems that permits to define the remaining coefficients \(c_3,\ldots,c_n\). One sees quickly that the coefficient \(c_k\) only depends on the interpolation points \((x_0,y_0),\ldots,(x_k,y_k)\), where \(y_i:=f(x_i)\), \(i=0,\ldots,n\).

We introduce the folllwing so-called finite difference notation for a function \(f\). The 0th order finite difference is defined to be \(f[x_0]:=f(x_0)\). The 1st order finite difference is

\[ f[x_0,x_1]:=\frac{f(x_1)-f(x_0)}{x_1-x_0}. \]

The second order finite difference is defined by

\[ f[x_0,x_1,x_2]:= \frac{f[x_1,x_2] - f[x_0,x_1]}{x_2-x_0}. \]

In general, the nth order finite difference of the function \(f\), also called the nth Newton divided difference, is defined recursively by

\[ f[x_0,\ldots,x_n]:= \frac{f[x_1,\ldots,x_n] - f[x_0,\ldots,x_{n-1}]}{x_n-x_0}. \]

Newton’s method to solve the polynomial interpolation problem can be summarized as follows. Given \(n+1\) interpolation points \((x_0,y_0),\ldots,(x_n,y_n)\), \(y_i:=f(x_i)\). If the order \(n\) interpolation polynomial is expressed in Newton’s form

\[ p_n(x)=c_n (x-x_0)(x-x_1)\cdots(x-x_{n-1}) + c_{n-1}(x-x_0)(x-x_1)\cdots(x-x_{n-2}) + \cdots + c_1(x-x_0) + c_0, \]

then the coefficients

\[ c_k = f[x_0,\ldots,x_k] \]

for \(k=0,\ldots,n\).

In fact, a recursion is in place

\[ p_n(x)=p_{n-1}(x) + f[x_0,\ldots,x_n](x-x_0)(x-x_1)\cdots(x-x_{n-1}) \]

It is common to write the finite differences in a table, which for \(n=3\) will look like:

\[\begin{split} \begin{array}{c|cccc} x_0 & f[x_0] & \\ & & f[x_0,x_1] & \\ x_1 & f[x_1] & & f[x_0,x_1,x_2] \\ & & f[x_1,x_2] & & f[x_0,x_1,x_2, x_3] \\ x_2 & f[x_2] & & f[x_1,x_2,x_3] \\ & & f[x_2,x_3] & \\ x_3 & f[x_3] \\ \end{array} \end{split}\]

Example 1 again: Given the points in Example 1. The corresponding table of divided differences becomes:

\[\begin{split} \begin{array}{c|cccc} 0 & 1 & \\ & & -3/4 & \\ 2/3 & 1/2 & & -3/4 \\ & & -3/2 & \\ 1 & 0 & \end{array} \end{split}\]

and the interpolation polynomial becomes

\[ p_2(x) = 1 - \frac{3}{4}(x-0)-\frac{3}{4}(x-0)(x-\frac23) = 1 - \frac{1}{4}x - \frac{3}{4} x^2. \]

73.2. Implementation

The method above is implemented as two functions:

• divdiff(xdata, ydata): Create the table of divided differences

• newtonInterpolation(F, xdata, x): Evaluate the interpolation polynomial.

Here, xdata and ydata are arrays with the interpolation points, and x is an array of values in which the polynomial is evaluated.

def divdiff(xdata, ydata):
    # Create the table of divided differences based
    # on the data in the arrays x_data and y_data.
    n = len(xdata)
    F = np.zeros((n, n))
    F[:, 0] = ydata  # Array for the divided differences
    for j in range(n):
        for i in range(n - j - 1):
            F[i, j + 1] = (F[i + 1, j] - F[i, j]) / (xdata[i + j + 1] - xdata[i])
    return F  # Return all of F for inspection.
    # Only the first row is necessary for the
    # polynomial.


def newton_interpolation(F, xdata, x):
    # The Newton interpolation polynomial evaluated in x.
    n, m = np.shape(F)
    xpoly = np.ones(len(x))  # (x-x[0])(x-x[1])...
    newton_poly = F[0, 0] * np.ones(len(x))  # The Newton polynomial
    for j in range(n - 1):
        xpoly = xpoly * (x - xdata[j])
        newton_poly = newton_poly + F[0, j + 1] * xpoly
    return newton_poly

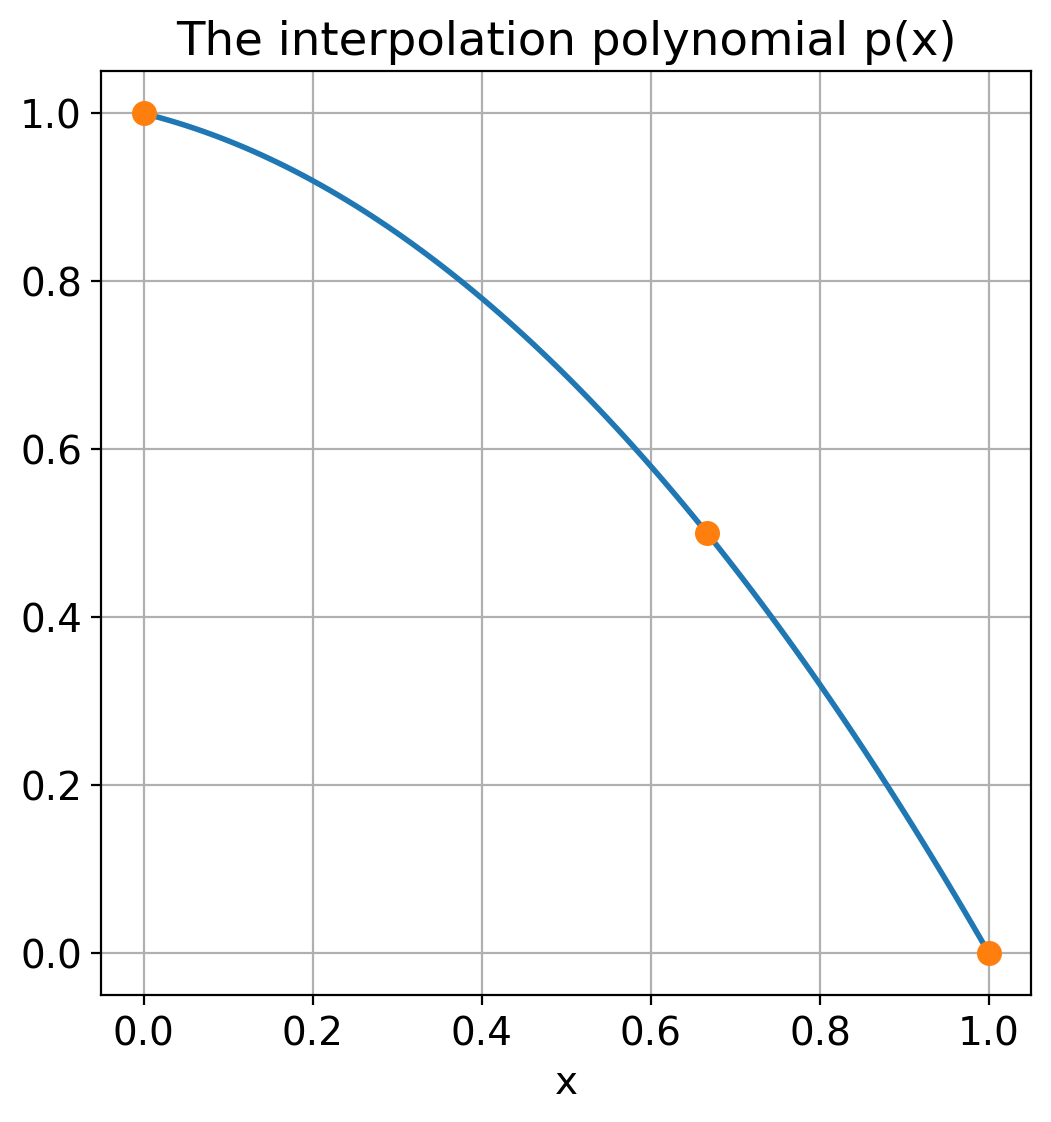
Run the code on the example above:

# Example: Use of divided differences and the Newton interpolation
# formula.
xdata = [0, 2 / 3, 1]
ydata = [1, 1 / 2, 0]
F = divdiff(xdata, ydata)  # The table of divided differences
print("The table of divided differences:\n", F)

x = np.linspace(0, 1, 101)  # The x-values in which the polynomial is evaluated
p = newton_interpolation(F, xdata, x)
plt.plot(x, p)  # Plot the polynomial
plt.plot(xdata, ydata, "o")  # Plot the interpolation points
plt.title("The interpolation polynomial p(x)")
plt.grid(True)
plt.xlabel("x");

The table of divided differences:
 [[ 1.   -0.75 -0.75]
 [ 0.5  -1.5   0.  ]
 [ 0.    0.    0.  ]]