Polynomial interpolation: Error theory

78. Polynomial interpolation: Error theory#

Anne Kværnø (modified by André Massing)

Date: Jan 21, 2021

If you want to have a nicer theme for your jupyter notebook, download the cascade stylesheet file tma4125.css and execute the next cell:

import matplotlib.pyplot as plt
import numpy as np
from IPython.core.display import HTML
from numpy import pi
from numpy.linalg import norm, solve  # Solve linear systems and compute norms


def css_styling():
    try:
        with open("tma4125.css") as f:
            styles = f.read()
            return HTML(styles)
    except FileNotFoundError:
        pass  # Do nothing


# Comment out next line and execute this cell to restore the default notebook style
css_styling()

And of course we want to import the required Modules.

%matplotlib inline


newparams = {
    "figure.figsize": (6.0, 6.0),
    "axes.grid": True,
    "lines.markersize": 8,
    "lines.linewidth": 2,
    "font.size": 14,
}
plt.rcParams.update(newparams)

Finally, we also run the LagrangePolynomial.ipynb to import the function cardinal and lagrange.

%run LagrangeInterpolation.ipynb

../_images/4b5c98eeb4ef41e26ff6625cd8289f71ab1ab88e7dfa4196213256d704f11bd1.png

../_images/139dd665ecfde12ebf0b75f8b158399a4dc7b441436c71e3cc1110248640f85c.png

79. Theory#

Given some function $f\in C[a,b]$. Choose $n+1$ distinct nodes in $[a,b]$ and let $p_n(x) \in \mathbb{P}_n$ satisfy the interpolation condition

\[ p_n(x_i) = f(x_i), \qquad i=0,\dots,n. \]

What can be said about the error $e(x)=f(x)-p_n(x)$?

The goal of this section is to cover a few theoretical aspects, and to give the answer to the natural question:

If the polynomial is used to approximate a function, can we find an expression for the error?
How can the error be made as small as possible?

Let us start with an numerical experiment, to have a certain feeling of what to expect.

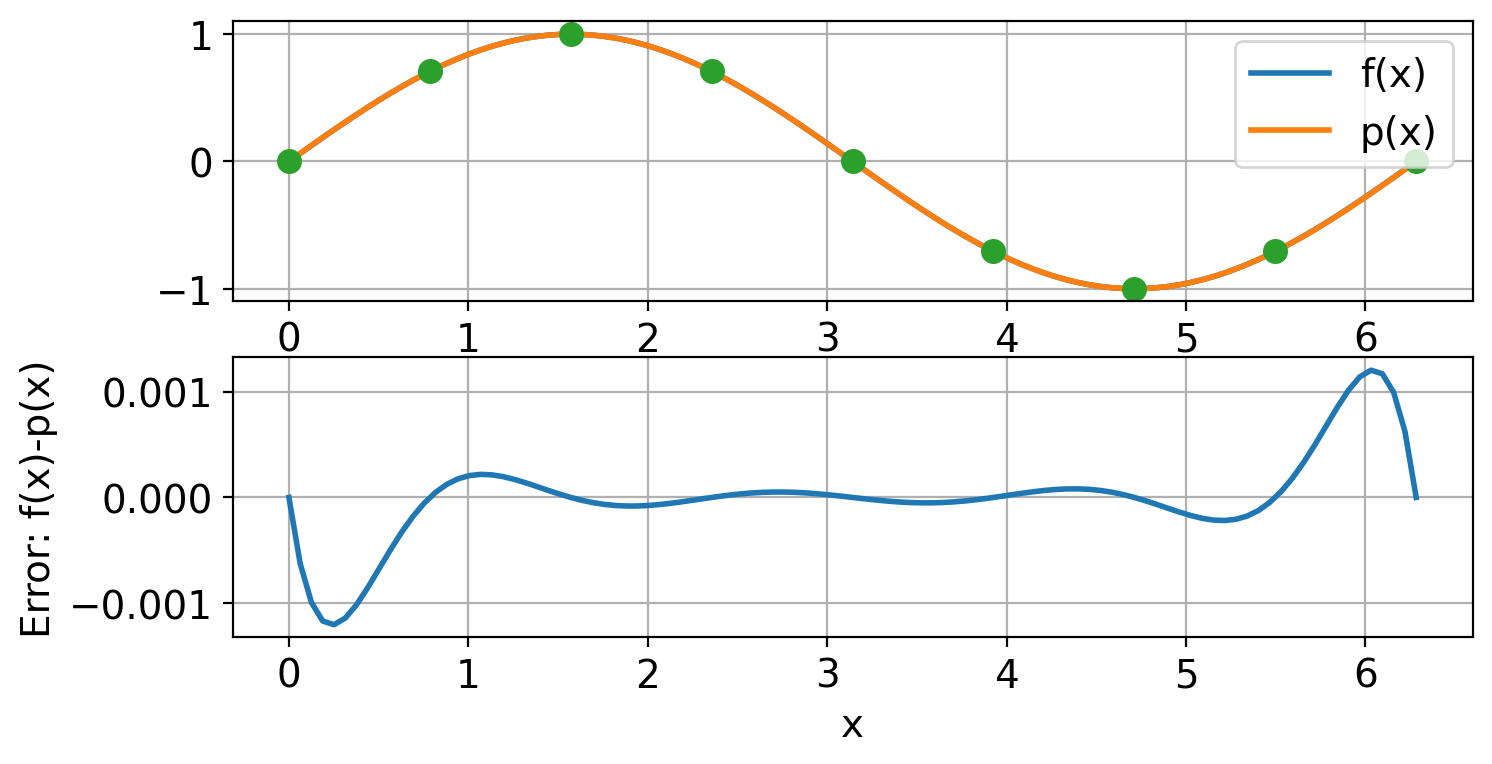
79.1. Example 1: Interpolation of $\sin x$#

Let $f(x)=\sin(x)$, $x\in [0,2\pi]$. Choose $n+1$ equidistributed nodes, that is $x_i=ih$, $i=0,\dots,n$, and $h=2\pi/n$. Calculate the interpolation polynomial by use of the functions `cardinal` and `lagrange`. Plot the error $e_n(x)=f(x)-p_n(x)$ for different values of $n$. Choose $n=4,8,16$ and $32$. Notice how the error is distributed over the interval, and find the maximum error $\max_{x\in[a,b]}|e_n(x)|$ for each $n$.

# Define the function


def f(x):
    return np.sin(x)


# Set the interval
a, b = 0, 2 * pi  # The interpolation interval
x = np.linspace(a, b, 101)  # The 'x-axis'

# Set the interpolation points
n = 8  # Interpolation points
xdata = np.linspace(a, b, n + 1)  # Equidistributed nodes (can be changed)
ydata = f(xdata)

# Evaluate the interpolation polynomial in the x-values
l = cardinal(xdata, x)
p = lagrange(ydata, l)

# Plot f(x) og p(x) and the interpolation points
plt.subplot(2, 1, 1)
plt.plot(x, f(x), x, p, xdata, ydata, "o")
plt.legend(["f(x)", "p(x)"])
plt.grid(True)

# Plot the interpolation error
plt.subplot(2, 1, 2)
plt.plot(x, (f(x) - p))
plt.xlabel("x")
plt.ylabel("Error: f(x)-p(x)")
plt.grid(True)
print(f"Max error is {max(abs(p - f(x))):.2e}")

Max error is 1.20e-03

../_images/84255b519b5f0ec72b77406b14ab3d87d0bce43a6af38f1978f222ee2c59f75b.png

79.2. Exercise 1: Interpolation of $\tfrac{1}{1+x^2}$#

Repeat the previous experiment with Runge’s function

\[ f(x) = \frac{1}{1+x^2}, \qquad x\in [-5,5]. \]

# Insert your code here

79.3. Error Analysis#

Taylor polynomials once more. Before we turn to the analysis of the interpolation error $e(x) = f(x) - p_n(x)$, we quickly recall (once more) Taylor polynomials and their error representation. For $f \in C^{n+1}[a,b]$ and $x_0 \in (a,b)$, we defined the $n$-th order Taylor polynomial $T^n_{x_0}f(x)$ of $f$ around $x_0$ by

\[ \begin{align*} T^n_{x_0}f(x) &:= \sum_{k=0}^{n} \frac{f^{(k)}(x_0)}{k!}(x-x_0)^k \end{align*} \]

Note that the Taylor polynomial is in fact a polynomial of order $n$ which not only interpolates $f$ in $x_0$, but also its first, second etc. and $n$-th derivative $f', f'', \ldots f^{(n)}$ in $x_0$!

So the Taylor polynomial the unique polynomial of order $n$ which interpolates the first $n$ derivatives of $f$ in a single point $x_0$. In contrast, the interpolation polynomial $p_n$ is the unique polynomial of order $n$ which interpolates only the $0$-order (that is, $f$ itself), but in $n$ distinctive points $x_0, x_1,\ldots x_n$.

For the Taylor polynomial $T^n_{x_0}f(x)$ we have the error representation

\[ \begin{align*} f(x) - T^n_{x_0}f(x) = R_{n+1}(x_0) \qquad \text{where } R_{n+1}(x_0) = \frac{f^{(n+1)}(\xi)}{(n+1)!} (x-x_0)^{n+1}, \end{align*} \]

with $\xi$ between $x$ and $x_0$.

Of course, we usually don’t know the exact location of $\xi$ and thus not the exact error, but we can at least estimate it and bound it from above:

\[ |f(x) - T^n_{x_0}f(x)| \leqslant \frac{M}{(n+1)!} h^{n+1} \]

where

\[ M=\max_{x\in[a,b]}|f^{(n+1)}(x)| \qquad \text{and} \qquad h = |x-x_0|. \]

The next theorem gives us an expression for the interpolation error $e(x)=f(x)-p_n(x)$ which is similar to what we have just seen for the error between the Taylor polynomial and the original function $f$.

79.4. Theorem 1: Interpolation error#

Given $f \in C^{(n+1)}[a,b]$. Let $p_{n} \in \mathbb{P}_n$ interpolate $f$ in $n+1$ distinct nodes $x_i \in [a,b]$. For each $x\in [a,b]$ there is at least one $\xi(x) \in (a,b)$ such that

\[ f(x) - p_n(x) = \frac{f^{(n+1)}(\xi(x))}{(n+1)!}\prod_{i=0}^n(x-x_i). \]

Proof. We start fromt the Newton polynomial $\omega_{n+1} =: \omega(x)$

\[ \omega(x) = \prod_{i=0}^{n}(x-x_i) = x^{n+1} + \dotsm. \]

Clearly, the error in the nodes, $e(x_i)=0$. Choose an arbitrary $x\in [a,b]$, $x\in [a,b]$, where $x\not=x_i$, $i=0,1,\dotsc,n$. For this fixed $x$, define a function in $t$ as:

\[ \varphi(t) = e(t)\omega(x) - e(x)\omega(t). \]

where $e(t) = f(t)-p_n(t)$.

Notice that $\varphi(t)$ is as differentiable with respect to $t$ as $f(t)$. The function $\varphi(t)$ has $n+2$ distinct zeros (the nodes and the fixed x). As a consequence of Rolle’s theorem, the derivative $\varphi'(t)$ has at least $n+1$ distinct zeros, one between each of the zeros of $\varphi(t)$. So $\varphi''(t)$ has $n$ distinct zeros, etc. By repeating this argument, we can see that $\varphi^{n+1}(t)$ has at least one zero in $[a,b]$, let us call this $\xi(x)$, as it does depend on the fixed $x$.

Since $\omega^{(n+1)}(t)=(n+1)!$ and $e^{(n+1)}(t)=f^{(n+1)}(t)$ we obtain

\[ \varphi^{(n+1)}(\xi)= 0 = f^{(n+1)}(\xi)\omega(x) - e(x)(n+1)! \]

which concludes the proof.

Observation. The interpolation error consists of three elements: The derivative of the function $f$, the number of interpolation points $n+1$ and the distribution of the nodes $x_i$. We cannot do much with the first of these, but we can choose the two others. Let us first look at the most obvious choice of nodes.

79.4.1. Equidistributed nodes#

The nodes are equidistributed over the interval $[a,b]$ if $x_i=a+ih$, $h=(b-a)/n$. In this case it can be proved that:

\[ |\omega(x)| \leq \frac{h^{n+1}}{4}n! \]

such that

\[ |e(x)| \leq \frac{h^{n+1}}{4(n+1)}M, \qquad M=\max_{x\in[a,b]}|f^{(n+1)}(x)|. \]

for all $x\in [a,b]$.

Let us now see how good this error bound is by an example.

79.5. Exercise 2: Interpolation error for $\sin(x)$ revisited#

Let again $f(x)=\sin(x)$ and $p_n(x)$ the polynomial interpolating $f(x)$ in $n+1$ equidistributed points on $[0,1]$. An upper bound for the error for different values of $n$ can be found easily. Clearly, $\max_{x\in[0,2\pi]}|f^{(n+1)}(x)|=M=1$ for all $n$, so

\[ |e_n(x)| = |f(x)-p_n(x)| \leq \frac{1}{4(n+1)}\left(\frac{2\pi}{n}\right)^{n+1}, \qquad x\in[a,b]. \]

Use the code in the first Example of this lecture to verify the result for $n = 2, 4, 8, 16$. How close is the bound to the real error?

# Insert your code here

79.6. Optimal choice of interpolation points#

So how can the error be reduced? For a given $n$ there is only one choice: to distribute the nodes in order to make $|\omega(x)|= \prod_{j=0}^{n}|x-x_i|$ as small as possible. We will first do this on a standard interval $[-1,1]$, and then transfer the results to some arbitrary interval $[a,b]$.

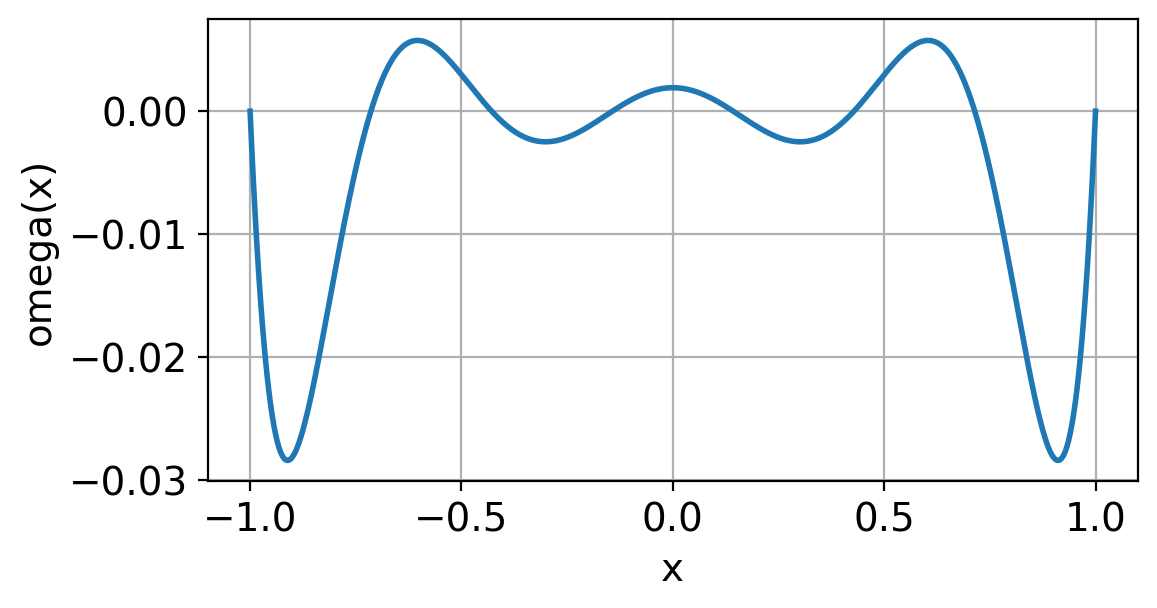
Let us start taking a look at $\omega(x)$ for equidistributed nodes on the interval $[-1,1]$, for different values of $n$:

newparams = {"figure.figsize": (6, 3)}
plt.rcParams.update(newparams)


def omega(xdata, x):
    # compute omega(x) for the nodes in xdata
    n1 = len(xdata)
    omega_value = np.ones(len(x))
    for j in range(n1):
        omega_value = omega_value * (x - xdata[j])  # (x-x_0)(x-x_1)...(x-x_n)
    return omega_value

# Plot omega(x)
n = 8  # Number of interpolation points is n+1
a, b = -1, 1  # The interval
x = np.linspace(a, b, 501)
xdata = np.linspace(a, b, n)
plt.plot(x, omega(xdata, x))
plt.grid(True)
plt.xlabel("x")
plt.ylabel("omega(x)")
print(f"n = {n:2d}, max|omega(x)| = {max(abs(omega(xdata, x))):.2e}")

n =  8, max|omega(x)| = 2.84e-02

../_images/a572ea006ccd07d0d7253e33f919657b8e520f215555ac875fd079792130a66f.png

Run the code for different values of $n$. Notice the following:

$\max_{x\in[-1,1]} |\omega(x)|$ becomes smaller with increasing $n$.
$|\omega(x)|$ has its maximum values near the boundaries of $[-1, 1]$.

A a consequence of the latter, it seems reasonable to move the nodes towards the boundaries. It can be proved that the optimal choice of nodes are the Chebyshev-nodes, given by

\[ \tilde{x}_i = \cos \left( \frac{(2i+1)\pi}{2(n+1)} \right), \qquad i=0,\dotsc,n \]

Let $\omega_{Cheb}(x) = \prod_{j=1}^n(x-\tilde{x}_i)$. It is then possible to prove that

\[ \frac{1}{2^{n}} = \max_{x\in [-1, 1]} |\omega_{Cheb}(x)| \leq \max_{x \in [-1, 1]} |q(x)| \]

for all polynomials $q\in \mathbb{P}_n$ such that $q(x)=x^n + c_{n-1}x^{n-1}+\dotsm+c_1x + c_0$.

The distribution of nodes can be transferred to an interval $[a,b]$ by the linear transformation

\[ x = \frac{b-a}{2}\tilde{x} + \frac{b+a}{2} \]

where $x\in[a,b]$ and $\tilde{x} \in [-1,1]$.

By doing so we get

\[ \omega(x) = \prod_{j=0}^n (x-x_i) = \left(\frac{b-a}{2}\right)^{n+1} \prod_{j=0}^n (\tilde{x}-\tilde{x}_i) = \left(\frac{b-a}{2}\right)^{n+1} \omega_{Cheb}(\tilde{x}). \]

From the theorem on interpolation errors we can conclude:

Theorem (interpolation error for Chebyshev interpolation).

Given $f \in C^{(n+1)}[a,b]$, and let $M_{n+1} = \max_{x\in [a,b]}|f^{(n+1)}(x)|$. Let $p_{n} \in \mathbb{P}_n$ interpolate $f$ i $n+1$ Chebyshev-nodes $x_i \in [a,b]$. Then

\[ \max_{x\in[a,b]}|f(x) - p_n(x)| \leq \frac{(b-a)^{n+1}}{2^{2n+1}(n+1)!} M_{n+1}. \]

The Chebyshev nodes over an interval $[a,b]$ are evaluated in the following function:

def chebyshev_nodes(a, b, n):
    # n Chebyshev nodes in the interval [a, b]
    i = np.array(range(n))  # i = [0,1,2,3, ....n-1]
    x = np.cos((2 * i + 1) * pi / (2 * (n)))  # nodes over the interval [-1,1]
    return 0.5 * (b - a) * x + 0.5 * (b + a)  # nodes over the interval [a,b]

79.7. Exercise 3: Chebyshev interpolation#

a) Plot $\omega_{Cheb}(x)$ for $3, 5, 9, 17$ interpolation points on the interval $[-1,1]$.

# Insert your code here

b) Repeat Example 3 using Chebyshev interpolation on the functions below. Compare with the results you got from equidistributed nodes.

\[\begin{split} \begin{align*} f(x) &= \sin(x), && x\in[0,2\pi] \\ f(x) &= \frac{1}{1+x^2}, && x\in[-5,5]. \end{align*} \end{split}\]

# Insert your code here

For information: Chebfun is software package which makes it possible to manipulate functions and to solve equations with accuracy close to machine accuracy. The algorithms are based on polynomial interpolation in Chebyshev nodes.

Polynomial interpolation: Error theory

Contents